|
Europhysics
News (2004) Vol. 35 No. 2
The
art of taming light: ultra-slow and stopped light
Zachary Dutton1,2, Naomi S. Ginsberg2,
Christopher Slowe2, and Lene Vestergaard Hau2
1 Lyman Laboratory, Harvard University, Cambridge MA 02138
2 Present address: National Institute of Standards and Technology,
Electron and Optical Division, Gaithersburg MD 20899-8410
In
1998, laser pulses were slowed [1] in a Bose-Einstein condensate (BEC)
[2] of sodium to only 17 m/s, more than seven orders of magnitude lower
than the speed of light in vacuum. Associated with the dramatic reduction
factor for the light speed was a spatial compression of the pulses by
the same large factor. A light pulse, which was more than 1 km long
in vacuum, was compressed to a size of ~50 Ám, and at that point was
completely contained within the condensate [1]. This allowed the light-slowing
experiments to be brought to their ultimate extreme [3]: in the summer
of 2000, light pulses were completely stopped, stored, and subsequently
revived in an atomic medium, with millisecond storage times [4]. The
initial ultra-slow light experiments spurred a flurry of slow light
investigations, and slow or partially stopped light has now been observed
in limited geometries in warm rubidium vapours [5-7], liquid-nitrogen
cooled crystals [8], and recently in room temperature crystals [9].
Here, we begin with a discussion of ultra-slow and
stopped light. We describe how cold atoms and Bose-Einstein condensates
have been manipulated to generate media with extreme optical properties.
While the initial experiments concentrated on the light propagation,
we have recently begun a number of investigations of the effects that
slow light has on the medium in which it propagates. Effects are profound
because both the velocity and length scales associated with propagating
light pulses have been brought down to match the characteristic velocity
and length scales of the medium. With the most recent extension, the
light roadblock [10], we have compressed light pulses to a length
of only 2 Ám. Here, we describe the use of ultra-compressed light pulses
to probe superfluidity and the creation of quantized vortices in BECs
through formation of 'superfluid shock waves'.
We also present the observation of an ultra-slow-light-based,
pulsed atom laser. Furthermore, we demonstrate the use of slow and stopped
light for manipulation of optical information, in particular in Bose-Einstein
condensates that allow for phase coherent processing of three-dimensional,
compressed patterns of stored optical information.
Ultra-slow light
In
our experiments we use a cloud of ultra-cold sodium atoms, trapped by
an electromagnet in an ultra-high vacuum chamber (Fig. 1a). By illuminating
the cloud with a precisely tuned 'coupling' laser beam, the optical
properties of the atoms can be dramatically altered so that a laser
pulse, subsequently sent through this coupled atom-light medium, will
move at very low velocity. By choosing the right polarisations of the
two laser beams, the light fields selectively couple three internal
energy levels of the atoms (Fig 1b).
Initially, the atoms are all in the ground state
labeled |1 , and the laser fields are off. The coupling laser is turned
on and couples |2 , and the laser fields are off. The coupling laser is turned
on and couples |2 to the upper state, |3 to the upper state, |3 . Since |2 . Since |2 is unpopulated,
the coupling laser is not absorbed but rather causes the upper energy
level, |3 is unpopulated,
the coupling laser is not absorbed but rather causes the upper energy
level, |3 , to split symmetrically into two new energy levels (Fig.
1b). The energy difference between these new states is proportional
to the magnitude of the electric field of the coupling laser. A 'probe'
light pulse, tuned to the |1 , to split symmetrically into two new energy levels (Fig.
1b). The energy difference between these new states is proportional
to the magnitude of the electric field of the coupling laser. A 'probe'
light pulse, tuned to the |1 -|3 -|3 transition, is injected into the BEC.
It is this light pulse that is compressed and propagates at ultra low
group velocity. A light detector (PMT in Fig. 1a) is used to measure
the arrival of the pulse as it exits the atom cloud. transition, is injected into the BEC.
It is this light pulse that is compressed and propagates at ultra low
group velocity. A light detector (PMT in Fig. 1a) is used to measure
the arrival of the pulse as it exits the atom cloud.
The refractive index profile for the probe pulse
in the slow-light medium is shown in Fig 1c. The refractive index on
resonance is unity-the value in free space-because the contributions
to the susceptibility from the two symmetrically split energy levels
exactly cancel. This results in a steep and linear refractive index
variation around the |1 -|3 -|3 resonance, which leads to low light speeds since the signal velocity
of a light pulse is inversely proportional to the refractive index slope.
With cold atoms there is a negligible Doppler smearing of the energy
levels and illumination with very low coupling intensities is possible.
This brings the split levels close together and creates very steep refractive
index slopes and extremely low light speeds. While the pulse is in the
atom cloud, its group velocity and spatial extent are both proportional
to the intensity of the coupling field and inversely proportional to
the atom density. These parameters can be experimentally controlled.
resonance, which leads to low light speeds since the signal velocity
of a light pulse is inversely proportional to the refractive index slope.
With cold atoms there is a negligible Doppler smearing of the energy
levels and illumination with very low coupling intensities is possible.
This brings the split levels close together and creates very steep refractive
index slopes and extremely low light speeds. While the pulse is in the
atom cloud, its group velocity and spatial extent are both proportional
to the intensity of the coupling field and inversely proportional to
the atom density. These parameters can be experimentally controlled.
A resonant probe pulse would be completely attenuated
in the atom cloud in the absence of the coupling laser. However, when
the coupling laser is present, a narrow transmission window is created
around resonance, and the pulses can propagate though the atom cloud.
This effect, electromagnetically induced transparency [11], is also
responsible for maintaining the very steep slopes of the refractive
index profile, even in the presence of spontaneous radiation damping
from the upper state, |3 ,
which would otherwise broaden the profile in Fig. 1c. It occurs due
to a quantum mechanical interference created in the atom-light system:
absorption of a probe photon is associated with the transition of an
atom from |1 ,
which would otherwise broaden the profile in Fig. 1c. It occurs due
to a quantum mechanical interference created in the atom-light system:
absorption of a probe photon is associated with the transition of an
atom from |1 to |3
to |3 .
However, there is another path to that final state, where the atom absorbs
a coupling photon and makes a transition from |2 .
However, there is another path to that final state, where the atom absorbs
a coupling photon and makes a transition from |2 to |3
to |3 .
As a result, when the atom is in a very particular quantum mechanical
superposition of |1 .
As a result, when the atom is in a very particular quantum mechanical
superposition of |1 and |2
and |2 ,
the transition amplitudes for the two paths cancel. In this 'dark state',
the atom absorbs from neither the probe nor the coupling laser fields,
and the amplitude for the atom to be in |2 ,
the transition amplitudes for the two paths cancel. In this 'dark state',
the atom absorbs from neither the probe nor the coupling laser fields,
and the amplitude for the atom to be in |2 relative to the amplitude for |1
relative to the amplitude for |1 ,
A2/A1, is proportional to minus the ratio of the electric field
amplitudes of the probe and coupling laser fields. This makes the process
phase sensitive: the ratio A2/A1 is a complex number that depends on
the relative phase of the probe and coupling fields. ,
A2/A1, is proportional to minus the ratio of the electric field
amplitudes of the probe and coupling laser fields. This makes the process
phase sensitive: the ratio A2/A1 is a complex number that depends on
the relative phase of the probe and coupling fields.
As the light pulse enters the atom cloud, the front
edge slows down, the back edge-still in free space-catches up and the
pulse spatially compresses. As the pulse propagates through the atom
cloud, the atoms within the spatially localized pulse region are in
dark superposition states. The spatial distribution of the dark states
mimics the spatial variation of the light pulse: the pulse makes an
imprint-a hologram, really-in the atom cloud and this imprint follows
the pulse as it slowly propagates. Eventually the light pulse and the
imprint reach the other end of the cloud where the front edge speeds
up and the pulse expands spatially. The light pulse reaches the same
shape as it had before it entered the medium, but is delayed by several
microseconds in a cloud of only 100-200 Ám (Fig 1d).
Fig. 2a shows images of the atomic imprint of a 2
Ás light pulse, with a length of 600 m in free space, as it compresses
and propagates into a 100 Ám long and 30 Ám wide, cigar-shaped Bose-Einstein
condensate. To photograph the pulse, we selectively image |2 atoms in the cloud with the 'imaging' laser beam shown in Fig.1a, revealing
the instantaneous shape of the imprint. The transverse width of the
probe laser beam (in the x-y plane) is larger than the size of
the condensate. The pulse is entering the cloud, and compressing, through
the first 5 Ás and then starts its slow propagation into the cloud.
The observed boomerang shape of the light pulse (at 5 Ás) reflects that
the light speed along the centreline of the condensate is significantly
lower than at the edges due to the high atom density in the middle of
the cloud.
atoms in the cloud with the 'imaging' laser beam shown in Fig.1a, revealing
the instantaneous shape of the imprint. The transverse width of the
probe laser beam (in the x-y plane) is larger than the size of
the condensate. The pulse is entering the cloud, and compressing, through
the first 5 Ás and then starts its slow propagation into the cloud.
The observed boomerang shape of the light pulse (at 5 Ás) reflects that
the light speed along the centreline of the condensate is significantly
lower than at the edges due to the high atom density in the middle of
the cloud.
Stopped light
Because of the aforementioned spatial compression, the light pulse is
eventually completely contained within the atom cloud. By an abrupt
turn-off of the coupling laser, the moving light pulse stops and turns
off, but leaves the holographic imprint frozen in the cloud [4]. Figure
2b shows a light-stopping experiment performed in a Bose-Einstein condensate,
with two probe light pulses incident on the condensate from opposite
directions. The light pulses are stopped in the atom cloud just before
they collide, resulting in an imprint with a double boomerang shape
(0 ms). Because of photon-induced recoils, that come from the coherent
transfer of atoms from |1 to |2
to |2 ,
the two 'boomerangs' are shot out at ▒ 45░, each with a velocity of
4.2 cm/s. This shows very directly that the process is coherent: to
reach |2 ,
the two 'boomerangs' are shot out at ▒ 45░, each with a velocity of
4.2 cm/s. This shows very directly that the process is coherent: to
reach |2 ,
the atoms absorb a probe photon and emit a coupling photon through stimulated
emission. If instead, |2 ,
the atoms absorb a probe photon and emit a coupling photon through stimulated
emission. If instead, |2 had been reached via spontaneous, incoherent emission from |3
had been reached via spontaneous, incoherent emission from |3 ,
the two ejected atom clouds would (on average) have been kicked out
along the ▒z-directions and would have had a velocity spread
comparable to the recoil velocity. ,
the two ejected atom clouds would (on average) have been kicked out
along the ▒z-directions and would have had a velocity spread
comparable to the recoil velocity.
|
|
|
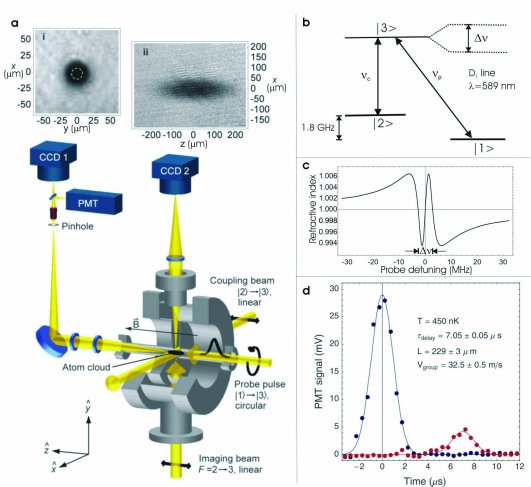
Fig 1 Ultra-Slow
Light
(a)
Experimental setup for generating slow and stopped light (from
ref. 1). The cigar-shaped, cooled atom cloud, consisting of sodium
atoms in state |1 (see (b)), is typically 100-200 Ám long and is trapped in an electromagnet.
The cloud is first illuminated from the side (along x)
by a coupling laser beam. The intensity and frequency of this
illuminating laser control the optical properties-in particular,
the refractive index profile and the transmission-for a probe
laser pulse subsequently sent into the medium (along z).
This light pulse then propagates extremely slowly through the
atom cloud. For propagation in a BEC, we obtain, with low coupling
laser power (12 mW/cm2), a light speed of only 17m/s.
The condensate would be completely opaque in the absence of the
coupling field, but the presence of this laser field allows transmission
of the light pulse (electromagnetically induced transparency).
A photo-multiplier tube (PMT) is used to measure the delay and
transmission of a probe pulse. The size of the atom cloud is determined
with use of a third laser, the 'imaging beam'. This laser beam
is sent into the system from below (along y) and the absorption
shadow of the atom cloud, created in the beam, is recorded on
a CCD camera (CCD2). An example is shown in inset (ii). Another
camera, CCD1, is used to image the cloud in the x-y plane. For
the slow and stopped light experiments (Figs 1 and 3), a pinhole
is placed in an external image plane so the PMT detects light
only that has been transmitted through the central 15 microns
of the condensate (indicated by the dashed circle in insert (i)).
(see (b)), is typically 100-200 Ám long and is trapped in an electromagnet.
The cloud is first illuminated from the side (along x)
by a coupling laser beam. The intensity and frequency of this
illuminating laser control the optical properties-in particular,
the refractive index profile and the transmission-for a probe
laser pulse subsequently sent into the medium (along z).
This light pulse then propagates extremely slowly through the
atom cloud. For propagation in a BEC, we obtain, with low coupling
laser power (12 mW/cm2), a light speed of only 17m/s.
The condensate would be completely opaque in the absence of the
coupling field, but the presence of this laser field allows transmission
of the light pulse (electromagnetically induced transparency).
A photo-multiplier tube (PMT) is used to measure the delay and
transmission of a probe pulse. The size of the atom cloud is determined
with use of a third laser, the 'imaging beam'. This laser beam
is sent into the system from below (along y) and the absorption
shadow of the atom cloud, created in the beam, is recorded on
a CCD camera (CCD2). An example is shown in inset (ii). Another
camera, CCD1, is used to image the cloud in the x-y plane. For
the slow and stopped light experiments (Figs 1 and 3), a pinhole
is placed in an external image plane so the PMT detects light
only that has been transmitted through the central 15 microns
of the condensate (indicated by the dashed circle in insert (i)).
(b) Three-level (L) system
of internal atomic states used to create slow light. The probe
and coupling laser beams are resonant with the |1 -|3 -|3 and |2
and |2 -|3 -|3 transitions, respectively, and couple the three states. Here,
np and nc
represent the resonance frequencies, and Dn
is the distance between the new split energy levels of the atom/coupling-laser
medium. Through the choice of frequencies and polarisations for
the probe and coupling lasers, we control which atomic states
participate in the process. The states used for the ultra-slow
light measurement in (d), obtained with the polarisations indicated
in (a), are |1
transitions, respectively, and couple the three states. Here,
np and nc
represent the resonance frequencies, and Dn
is the distance between the new split energy levels of the atom/coupling-laser
medium. Through the choice of frequencies and polarisations for
the probe and coupling lasers, we control which atomic states
participate in the process. The states used for the ultra-slow
light measurement in (d), obtained with the polarisations indicated
in (a), are |1 =|3S,F=1,MF=-1 =|3S,F=1,MF=-1 ,
|2 ,
|2 =|3S,F=2,MF=-2 =|3S,F=2,MF=-2 ,
and |3 ,
and |3 =|3P3/2,F=2,MF=-2 =|3P3/2,F=2,MF=-2 . .
(c)
Refractive index profile. We show the refractive index for the
probe laser as a function of its detuning from the |1 -|3 -|3 resonance frequency. Note that the refractive index on resonance
is unity, the value in free space. Importantly, the refractive
index has a very steep slope around resonance, and since the group
velocity of a light pulse is inversely proportional to that slope,
the profile shown leads to ultra-slow light. The figure was obtained
for a coupling intensity of 12 mW/cm2 and an atomic
density of 3.3.1012/cm3.
resonance frequency. Note that the refractive index on resonance
is unity, the value in free space. Importantly, the refractive
index has a very steep slope around resonance, and since the group
velocity of a light pulse is inversely proportional to that slope,
the profile shown leads to ultra-slow light. The figure was obtained
for a coupling intensity of 12 mW/cm2 and an atomic
density of 3.3.1012/cm3.
(d)
Observation of ultra-slow light (ref. 1). The blue data points
represent a reference pulse recorded with no atoms in the system
and used to set the zero-point for the time axis. The red data
points show a pulse that has propagated through an atom cloud
cooled to 450 nK which is just above the transition temperature
for BEC (the peak atomic density, in the cloud centre, is 3.3o1012/cm3).
In this case the delay of the light pulse is 7 Ás, in a cloud
that is only 229 Ám long (see insert (ii) in (a)). This results
in a light speed of 32 m/s which is seven orders of magnitude
below the value in free space.
|
Since the slow-light and light-storage
process is coherent, the ejected imprints are small condensates of |2 atoms. The observed changes in shape of the imprints as a function of
time, as shown in Fig 2b, are indeed in agreement with calculations
of condensate dynamics, based upon mean-field theory [12]. In effect,
we have created a pulsed atom laser with a controllable spatial mode
and a well-defined output-coupling velocity. Such an ultra-slow-light-based
atom laser could be used as a source for a high-brightness atom interferometer.
Such interferometers are beginning to rival classical precision measuring
devices including navigational gyroscopes [13] and gravitometers [14].
atoms. The observed changes in shape of the imprints as a function of
time, as shown in Fig 2b, are indeed in agreement with calculations
of condensate dynamics, based upon mean-field theory [12]. In effect,
we have created a pulsed atom laser with a controllable spatial mode
and a well-defined output-coupling velocity. Such an ultra-slow-light-based
atom laser could be used as a source for a high-brightness atom interferometer.
Such interferometers are beginning to rival classical precision measuring
devices including navigational gyroscopes [13] and gravitometers [14].
We have also studied the case of stopped light for
co-propagating coupling and probe laser beams with opposite circular
polarisations. In this case, photon-recoil effects are negligible, and
atoms in |2 are trapped by the electromagnet similarly to atoms in
|1 are trapped by the electromagnet similarly to atoms in
|1 . The holographic imprint of the stopped light pulse therefore stays
in the cloud for a long time. By switching the coupling field back on,
the amplitude and phase of the atomic wavefunctions are written back
onto the probe field, and the light pulse is revived after a long storage
time in the medium. . The holographic imprint of the stopped light pulse therefore stays
in the cloud for a long time. By switching the coupling field back on,
the amplitude and phase of the atomic wavefunctions are written back
onto the probe field, and the light pulse is revived after a long storage
time in the medium.
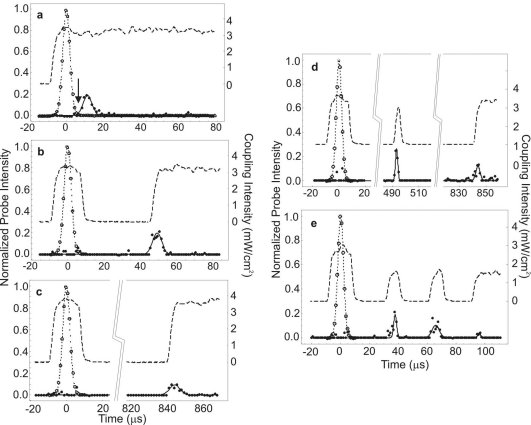
Fig. 3a shows a slow-light measurement with this
setup, performed in a cold atom cloud cooled to 900 nK (which is just
above the transition temperature for Bose-Einstein condensation). The
pulse delay is 12 Ás, and the arrow indicates the point in time when
the light pulse is slowed, compressed, and totally contained in the
middle of the atom cloud. In Figs 3b-c we abruptly turn the coupling
laser off at this time and freeze a holographic imprint in the cloud.
Since the imprint contains all the amplitude and phase information of
the original light pulse, we can later revive the light pulse and send
it back on its way, by simply turning the coupling laser back on. The
storage times for the light pulse are 38 Ás (Fig. 3b) and 833 Ás (Fig.
3c), respectively.
The revived light pulses can also be manipulated
[4]. In Figs 3d-e, a single light pulse is stored in the atom cloud
and later regenerated in two (Fig. 3d), and even three, small pieces
(Fig. 3e) by switching the coupling laser on and off several times.
Furthermore, we have observed that by turning the coupling laser back
on at a higher (lower) intensity, a temporally shorter (longer) light
pulse can be regenerated. In the language of optical engineering, the
bandwidth of the system can be manipulated dynamically, even for Fourier
transform limited pulse propagation.
The storage times for compressed optical information
are limited due to thermal smearing of the stored imprints, and are
optimised with the ultra-cold clouds we are using. For the parameters
in Figs 3, the storage time was limited to a few milliseconds.
Coherent processing
of optical information
This storage time can be increased dramatically with optical storage
in Bose-Einstein condensates, which are phase coherent objects. Furthermore,
the dynamics of the condensates during the storage time can be utilised
for processing of the stored optical information. The dynamics change
the spatial structure of the ground state coherences-the dark states-leading
to regenerated probe pulses with amplitude and phase changes that reflect
the dynamics.
|
|
|
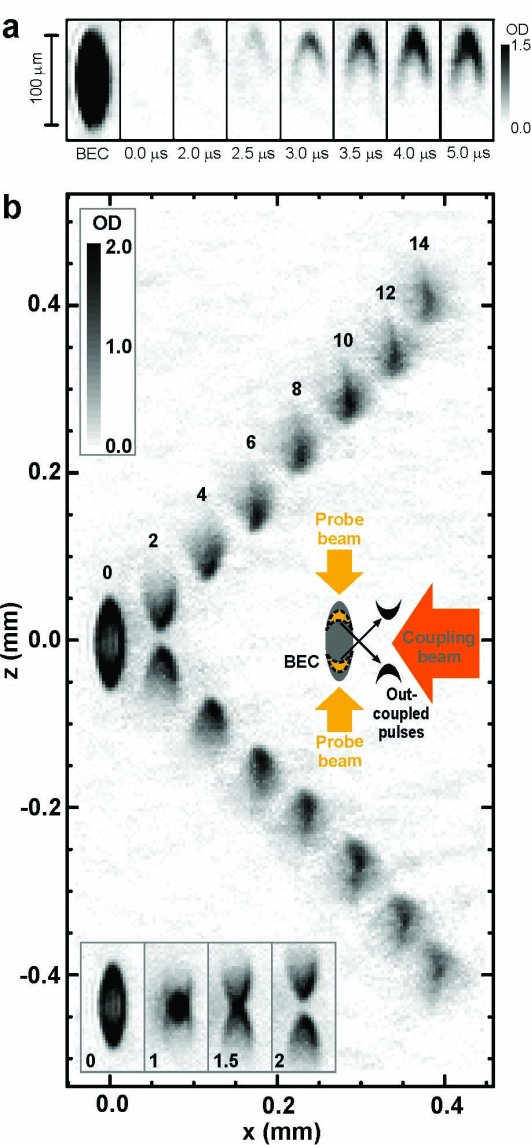
Fig 2 Atom
Laser with Ultra-Slow and Stopped Light
(a)
Observation of the slow-down and spatial compression of a light
pulse in a BEC. Setup is as in Fig 1a. The first figure ('BEC')
shows a condensate of |1 atoms, imaged before the light pulse is sent in. The picture is
taken with the imaging beam and recorded on CCD2. The condensate
is subsequently illuminated with the coupling laser and the probe
light pulse is sent into the atom cloud. As described in the text,
within the light pulse region, the atoms are in coherent dark
states that are superpositions of |1
atoms, imaged before the light pulse is sent in. The picture is
taken with the imaging beam and recorded on CCD2. The condensate
is subsequently illuminated with the coupling laser and the probe
light pulse is sent into the atom cloud. As described in the text,
within the light pulse region, the atoms are in coherent dark
states that are superpositions of |1 and |2
and |2 .
The spatial distribution of the dark states mimics the spatial
shape of the light pulse. This atomic imprint, created by the
light fields, travels with the light pulse. By selectively imaging
the density of atoms in |2 .
The spatial distribution of the dark states mimics the spatial
shape of the light pulse. This atomic imprint, created by the
light fields, travels with the light pulse. By selectively imaging
the density of atoms in |2 (on CCD2), we can thus image the light pulse as it propagates
through the condensate. The following pictures (from 0 Ás to 5
Ás) show such images of the light pulse as it propagates into
the atom cloud and spatially compresses. At 0 Ás, we start inputting
the front edge of the light pulse. After 5 Ás, the pulse is fully
input, compressed, and totally contained within the cloud. The
pulse starts out in free space, with a Gaussian shape and a length
of 1 km, and is compressed in the condensate to only 25 Ám. The
light pulse is also seen to develop a 'boomerang' shape. The probe
laser beam is uniform across the cloud in the x-direction (in
the y-direction, the beam is only 20 Ám wide to minimize smearing
of the pulse shape in the images), and in the middle of the condensate,
where the atom density is high, the pulse travels significantly
slower than at the edge of the cloud, where the density is low,
creating the boomerang shape. The grey-scale indicates the on-resonance
optical density (OD) of the images, obtained as minus the natural
logarithms of the transmission coefficient.
(on CCD2), we can thus image the light pulse as it propagates
through the condensate. The following pictures (from 0 Ás to 5
Ás) show such images of the light pulse as it propagates into
the atom cloud and spatially compresses. At 0 Ás, we start inputting
the front edge of the light pulse. After 5 Ás, the pulse is fully
input, compressed, and totally contained within the cloud. The
pulse starts out in free space, with a Gaussian shape and a length
of 1 km, and is compressed in the condensate to only 25 Ám. The
light pulse is also seen to develop a 'boomerang' shape. The probe
laser beam is uniform across the cloud in the x-direction (in
the y-direction, the beam is only 20 Ám wide to minimize smearing
of the pulse shape in the images), and in the middle of the condensate,
where the atom density is high, the pulse travels significantly
slower than at the edge of the cloud, where the density is low,
creating the boomerang shape. The grey-scale indicates the on-resonance
optical density (OD) of the images, obtained as minus the natural
logarithms of the transmission coefficient.
(b)
Atom laser. For this experiment we send two counter-propagating
probe light pulses into a Bose-Einstein condensate where they
are stopped and form the double-boomerang imprint in the cloud
labeled '0'. (The numbers in the figure indicate the times, in
milliseconds, after the light pulses are input and stopped). Again,
we selectively image the density of |2 atoms. To reach |2
atoms. To reach |2 ,
the atoms have absorbed a probe photon and, through stimulated
emission, emitted a coupling photon, leading to a ▒ 45░
photon-induced recoil of the |2 ,
the atoms have absorbed a probe photon and, through stimulated
emission, emitted a coupling photon, leading to a ▒ 45░
photon-induced recoil of the |2 atoms. We clearly see the two recoiling, boomerang-shaped imprints
of |2
atoms. We clearly see the two recoiling, boomerang-shaped imprints
of |2 atoms as they are kicked out of the condensate (2-14 ms) with
a velocity of 4.2 cm/s. They cross at 1 ms as shown in the inset.
At 2 ms, the imprints are separated again but still maintain their
boomerang shape. Since the slow-light and storage process is fully
coherent (as confirmed by the recoil directions), and the atom
imprints are output-coupled from a condensate, the ejected atom
clouds are condensates of |2
atoms as they are kicked out of the condensate (2-14 ms) with
a velocity of 4.2 cm/s. They cross at 1 ms as shown in the inset.
At 2 ms, the imprints are separated again but still maintain their
boomerang shape. Since the slow-light and storage process is fully
coherent (as confirmed by the recoil directions), and the atom
imprints are output-coupled from a condensate, the ejected atom
clouds are condensates of |2 atoms. This is confirmed by studying the ensuing dynamics. The
associated shape changes as a function of time agree with a Gross-Pitaevskii
mean-field description[12] of condensate dynamics. Between the
boomerang arms, a narrow 'snout' of atoms forms, which is clearly
seen sticking upward (on the upper track) at 10 and 12 ms. This
sharp feature is due to an interference between atoms moving inward
from the two boomerang arms. With this setup, we have created
a pulsed atom laser with spatially controlled output coupling.
In the case shown, there are 5 million atoms in the initial condensate
of |1
atoms. This is confirmed by studying the ensuing dynamics. The
associated shape changes as a function of time agree with a Gross-Pitaevskii
mean-field description[12] of condensate dynamics. Between the
boomerang arms, a narrow 'snout' of atoms forms, which is clearly
seen sticking upward (on the upper track) at 10 and 12 ms. This
sharp feature is due to an interference between atoms moving inward
from the two boomerang arms. With this setup, we have created
a pulsed atom laser with spatially controlled output coupling.
In the case shown, there are 5 million atoms in the initial condensate
of |1 atoms, and each output coupled condensate of |2
atoms, and each output coupled condensate of |2 atoms contain 225,000 atoms.
atoms contain 225,000 atoms.
|
We have developed a comprehensive formalism
to study these effects [15,16] and examples are shown in Fig. 4. Storing
a slowed light pulse in a BEC creates a two-component condensate, a
mixture of |1 and |2 and |2 atoms. The ensuing dynamics include nonlinear
atom-atom interactions between the two condensate components. Our formalism,
based on self-consistent Maxwell and condensate mean-field equations,
describes a two-component BEC exposed to coupling and probe laser fields. atoms. The ensuing dynamics include nonlinear
atom-atom interactions between the two condensate components. Our formalism,
based on self-consistent Maxwell and condensate mean-field equations,
describes a two-component BEC exposed to coupling and probe laser fields.
In Fig. 4a, the condensate component of |1 atoms
creates a mean-field repulsive potential for the component of |2 atoms
creates a mean-field repulsive potential for the component of |2 atoms.
The sum of the magnetic trapping potential and this mean field forms
an effective potential with sharp edges. The |2 atoms.
The sum of the magnetic trapping potential and this mean field forms
an effective potential with sharp edges. The |2 condensate reflects
off this boundary, which leads to formation of interference fringes
in the density of |2 condensate reflects
off this boundary, which leads to formation of interference fringes
in the density of |2 atoms. Remarkably, by subsequent turn-on of the
coupling laser, these complicated structures are written, with high
fidelity, onto a revived probe pulse (Fig. 4b). atoms. Remarkably, by subsequent turn-on of the
coupling laser, these complicated structures are written, with high
fidelity, onto a revived probe pulse (Fig. 4b).
Unlike the above example, which utilises a weak probe
field, a different regime is represented by Figs 4c-d where a strong
probe pulse, of about the same peak electric field amplitude as that
of the coupling field, propagates into a condensate and is stored (Fig.
4c). In this case, the slow-light and storage process significantly
changes the density of both condensate components, and this leads to
strong nonlinearities in the condensate dynamics. In Fig. 4d (left),
the two components are seen to phase-separate, and two dark solitons
are spontaneously formed in the condensate of |1 atoms, with the associated
density dips filled by |2 atoms, with the associated
density dips filled by |2 atoms. (Solitons are excitations that maintain
their shape due to a perfect balance between dispersion of collective
excitations and nonlinear atom-atom interactions. Dark solitons give
rise to a depletion of the atom density [17] as opposed to bright solitons
where the density is enhanced). The result is extremely stable, filled
'vector solitons' [18,19]. Due to phase gradients in the condensate,
the vector solitons move around and interact with each other. Upon subsequent
pulse revival, the relative amplitude and phase of the two-component
condensate, including the solitons, are written onto and transferred
to the light fields (Fig 4d, right panel). We see that in this strong
probe case, the coupling light field is also strongly affected by the
atom dynamics. atoms. (Solitons are excitations that maintain
their shape due to a perfect balance between dispersion of collective
excitations and nonlinear atom-atom interactions. Dark solitons give
rise to a depletion of the atom density [17] as opposed to bright solitons
where the density is enhanced). The result is extremely stable, filled
'vector solitons' [18,19]. Due to phase gradients in the condensate,
the vector solitons move around and interact with each other. Upon subsequent
pulse revival, the relative amplitude and phase of the two-component
condensate, including the solitons, are written onto and transferred
to the light fields (Fig 4d, right panel). We see that in this strong
probe case, the coupling light field is also strongly affected by the
atom dynamics.
It is now clear that by controlling the coupling
beam parameters, the shape and size of the outgoing probe pulses can
be manipulated, and mapping between atomic and light media can be performed
with high fidelity [15]. In the weak-probe limit and for certain atom-atom
interaction parameters, the |2 atoms experience, during the storage
time, a predictable trapping potential with its own set of eigenstates.
By choosing an incoming probe pulse profile that corresponds to one
of these eigenstates, the amplitude of the stored imprint is stationary,
and the imprint will evolve purely in phase. This setup could form the
basis for a one-bit phase shifting gate. If the initial pulse is not
a pure eigenstate of the system, as in Fig. 4a, it can be represented
by a superposition of eigenstates that will evolve independently and
lead to deterministic reshaping of the revived light pulse. Inputting
stronger probe pulses leads to nonlinear evolution in the condensate
which can be used for nonlinear processing of pulses. For example, one
could input two spatially separated light pulses and the ensuing evolution
will cause them to interact and introduce additional phase shifts on
each other. This is the ingredient necessary to construct a two-bit
conditional phase gate-a fundamental building block of quantum (or optical)
computation. Furthermore, atom-atom interactions can be controlled with
external electric and magnetic fields [20,21], with the exciting potential
for dynamically controlled processing of stored optical information. atoms experience, during the storage
time, a predictable trapping potential with its own set of eigenstates.
By choosing an incoming probe pulse profile that corresponds to one
of these eigenstates, the amplitude of the stored imprint is stationary,
and the imprint will evolve purely in phase. This setup could form the
basis for a one-bit phase shifting gate. If the initial pulse is not
a pure eigenstate of the system, as in Fig. 4a, it can be represented
by a superposition of eigenstates that will evolve independently and
lead to deterministic reshaping of the revived light pulse. Inputting
stronger probe pulses leads to nonlinear evolution in the condensate
which can be used for nonlinear processing of pulses. For example, one
could input two spatially separated light pulses and the ensuing evolution
will cause them to interact and introduce additional phase shifts on
each other. This is the ingredient necessary to construct a two-bit
conditional phase gate-a fundamental building block of quantum (or optical)
computation. Furthermore, atom-atom interactions can be controlled with
external electric and magnetic fields [20,21], with the exciting potential
for dynamically controlled processing of stored optical information.
|
|
|
Fig 3 Stopped
Light
(a)
Slow light pulse observed as in Fig. 1d. However, in this case,
the probe and coupling lasers are co-propagating and have opposite
circular polarisations. The L system
here has |2 =|3S,F=2,MF=+1 =|3S,F=2,MF=+1 and |3
and |3 =|3P1/2,F=2,MF=0 =|3P1/2,F=2,MF=0 .
There is no photon recoil and both |1 .
There is no photon recoil and both |1 and |2
and |2 are trapped by the magnet (|1
are trapped by the magnet (|1 and |2
and |2 have opposite gyro-magnetic ratios). In the figure, open circles
represent a measured reference pulse, and solid dots represent
a pulse measured after it has been delayed by 12 Ás in a cold
cloud (900 nK with peak density 1013/cm3).
The dashed curve shows the intensity of the coupling laser which
is turned on just a few microseconds before the probe pulse is
sent in. The arrow indicates the point in time when the pulse
is slowed, compressed, and contained in the middle of the cloud.
have opposite gyro-magnetic ratios). In the figure, open circles
represent a measured reference pulse, and solid dots represent
a pulse measured after it has been delayed by 12 Ás in a cold
cloud (900 nK with peak density 1013/cm3).
The dashed curve shows the intensity of the coupling laser which
is turned on just a few microseconds before the probe pulse is
sent in. The arrow indicates the point in time when the pulse
is slowed, compressed, and contained in the middle of the cloud.
(b-c) Observation of stopped
light. At the point in time indicated by the arrow in (a), we
abruptly turn off the coupling laser, with the result that no
probe pulse emerges. Some 38 Ás later (b), we turn the coupling
laser back on, and a light pulse is observed, with the same shape
and intensity as measured in (a). Clearly, in this case, we have
stopped the pulse and later revived it. In (c) we perform the
same experiment as in (b) except we store the imprint in the cloud
for 833 Ás before we revive the light pulse.
(d-e) Manipulation of stored
optical information. Here we inject and stop a single light pulse
in the atom cloud. By switching the coupling laser on and off
several times, we regenerate the light pulse in two small pieces
(d) and even in three small pieces (e). The probe pulse intensity
in the figures is normalised to the peak intensity of the reference
pulse. Figs (a-e) are from ref. 4.
|
Following the storage of a classical
light pulse in a BEC, condensate dynamics could develop non-classical
entangled-atom states [22,23]. By subsequently reviving the light pulse
[24], we could generate non-classical light fields from purely classical
input fields. The storage and revival of non-classical light fields,
with controlled processing during the storage time, as described above,
could be of great importance for quantum information processing where
the transfer between flying qubits (photons for example) and stationary
storage devices (atoms for example) is of paramount importance [25].
The light roadblock
and superfluid dynamics
We now turn our attention to the description of how slow light can be
used for direct probing of superfluid properties of Bose-Einstein condensates.
By spatial modulation of the coupling laser intensity along the propagation
direction of the probe pulses [10], we can, for example, control the
speed and spatial extent of light pulses as they are propagating through
the atom cloud. By spatially cutting off the coupling laser in the middle
of the condensate, we form a light roadblock: a probe pulse slows
down and compresses dramatically as it is running into the region of
very low coupling intensity (Fig. 5a). With this method, light pulses
1 km-long in free space are compressed to 2 Ám in a Bose-Einstein condensate.
Within the localised pulse region at the roadblock, the atoms are driven
almost entirely into |2 (the dark state when the coupling intensity goes to zero). As discussed
above (Fig. 2b), the localised 'defect' of |2
(the dark state when the coupling intensity goes to zero). As discussed
above (Fig. 2b), the localised 'defect' of |2 atoms is kicked out of the magnet in less than a millisecond, due to
photon recoil.
atoms is kicked out of the magnet in less than a millisecond, due to
photon recoil.
In the electromagnet, we are thus left with a |1 -atom
condensate with a slice punched in the middle. This void is so localised
that it is comparable to the condensate's healing length, the length
over which a superfluid can adjust to external perturbations [26]. The
density depletion of the condensate breaks into two density dips that
move at the local sound speed towards the condensate boundaries. Since
the density defects are narrow and deep, nonlinearities from atom-atom
interactions lead to a steepening of their back edges during propagation
in the condensate, which results in 'quantum shock waves' [10], the
superfluid analogue of shock waves in a classical fluid. -atom
condensate with a slice punched in the middle. This void is so localised
that it is comparable to the condensate's healing length, the length
over which a superfluid can adjust to external perturbations [26]. The
density depletion of the condensate breaks into two density dips that
move at the local sound speed towards the condensate boundaries. Since
the density defects are narrow and deep, nonlinearities from atom-atom
interactions lead to a steepening of their back edges during propagation
in the condensate, which results in 'quantum shock waves' [10], the
superfluid analogue of shock waves in a classical fluid.
An experimental observation of this process is shown
in Fig. 5b (from ref. 10). A narrow density defect is created at the
light roadblock, which immediately leads to formation of dark solitons
(white stripes at 0 ms). However, the solitons are unstable and their
fronts start to curl up, as seen at 0.5 ms. Subsequently, the points
along the main front, with the largest curvature, act as nucleation
sites for vortices with quantized circulation [26]. Vortices are observed
at 2.5 ms and are seen as white 'dots' where the condensate density
vanishes. Quantized vortices are very stable excitations of the superfluid
condensate. They are clearly seen at 11 ms, for example.
By means of shock-wave formation, vortices are created
far out of equilibrium, in pairs of opposite circulation, like particle
anti-particle pairs. Changing the length and intensity of a light pulse
sent towards the light roadblock adjusts the number of vortices formed.
Hence, we can controllably form many-body systems of vortices and study
their collision dynamics: in some cases the vortices collide like billiard
balls, in other cases their collisions lead to annihilation and the
energy is released in the form of outgoing sound waves.
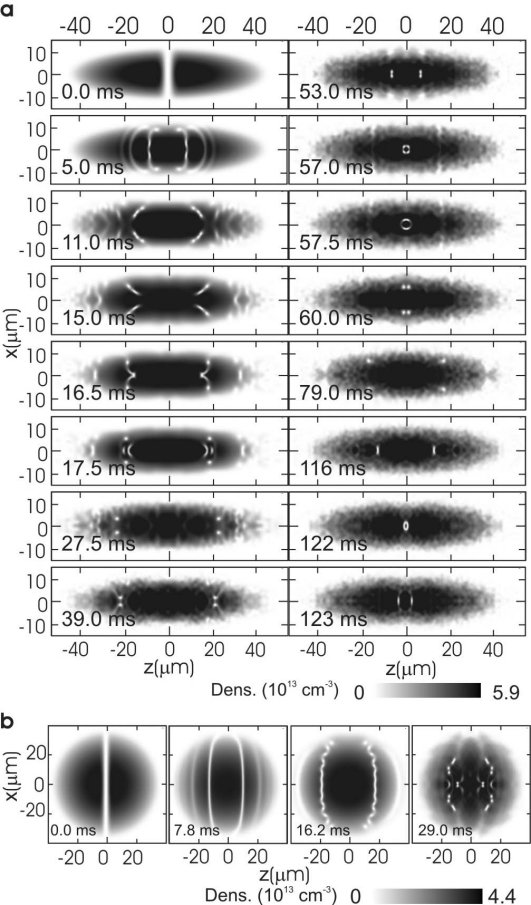
An example is shown in Fig. 6a, which is the result
of a numerical simulation of vortex dynamics in two dimensions, for
realistic experimental parameters. After a narrow defect is created
at the light roadblock, a total of 12 vortices are nucleated (11 ms).
Examination of the phase pattern of the condensate wavefunction reveals
that the vortices are singly quantized. They are created in pairs of
opposite circulation, with each vortex pair located at opposite sides
of the horizontal symmetry axis (x=0). The three vortices in
each quadrant spin around each other due to the velocity fields of adjacent
vortices, two out of each triplet annihilate, and the energy is carried
off as sound waves (seen as curved fronts at 16.5 ms and 17.5 ms).
|
|
|
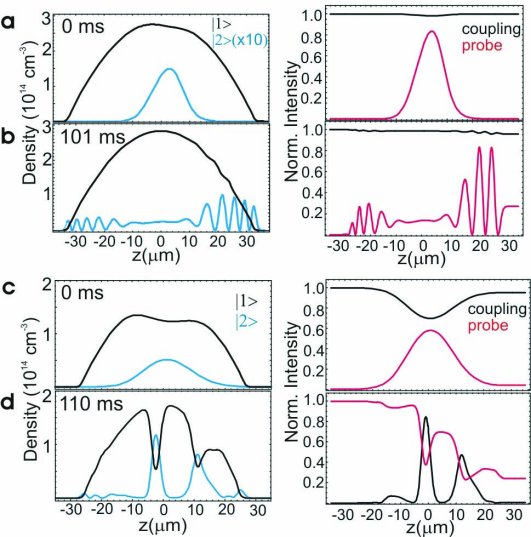
Fig 4 Coherent
Processing of Optical Information
The
calculations are performed for 87Rb (note that all
other figures are for sodium). Rubidium has scattering rates,
for inelastic scattering between the hyperfine ground states |1 and |2
and |2 (of the L system), that are lower than
those in sodium by two orders of magnitude [30]. Rubidium is therefore
particularly well suited for coherent processing over long time
scales.
(of the L system), that are lower than
those in sodium by two orders of magnitude [30]. Rubidium is therefore
particularly well suited for coherent processing over long time
scales.
(a-b) Weak probe case. A probe
pulse is injected into a BEC under ultra-slow-light conditions
and subsequently stopped in the condensate (at 0 ms). The corresponding
densities of |1 (black) and |2
(black) and |2 (blue) condensate atoms are shown in the left panel of (a). Coherent
two-component condensate dynamics, with atom-atom interactions
playing a major role, will effectively process the stored light
pulse information. In the example shown here, the condensate component
of |2
(blue) condensate atoms are shown in the left panel of (a). Coherent
two-component condensate dynamics, with atom-atom interactions
playing a major role, will effectively process the stored light
pulse information. In the example shown here, the condensate component
of |2 atoms will scatter off the sharp potential edge formed by the
magnetic trapping potential in combination with the repulsive
mean-field potential from the |1
atoms will scatter off the sharp potential edge formed by the
magnetic trapping potential in combination with the repulsive
mean-field potential from the |1 component. The reflected condensate component interferes with
itself and forms interference fringes in the density of |2
component. The reflected condensate component interferes with
itself and forms interference fringes in the density of |2 atoms (b). The right panels show the results of switching the
coupling laser back on at 0 ms and at 101 ms, respectively. Remarkably,
the complicated interference pattern in the |2
atoms (b). The right panels show the results of switching the
coupling laser back on at 0 ms and at 101 ms, respectively. Remarkably,
the complicated interference pattern in the |2 condensate is written onto the probe light field with high fidelity
(the red curve represents the probe intensity normalised to the
peak intensity of the input pulse). The coupling intensity (normalised
to the input intensity and shown as the black curve) is hardly
affected. We use co-propagating probe and coupling laser beams
with opposite circular polarisations such that the states forming
the L system are |1
condensate is written onto the probe light field with high fidelity
(the red curve represents the probe intensity normalised to the
peak intensity of the input pulse). The coupling intensity (normalised
to the input intensity and shown as the black curve) is hardly
affected. We use co-propagating probe and coupling laser beams
with opposite circular polarisations such that the states forming
the L system are |1 =|5S,F=2,MF=+1 =|5S,F=2,MF=+1 ,
|2 ,
|2 =|5S,F=1,MF=-1 =|5S,F=1,MF=-1 ,
and |3 ,
and |3 =|5P1/2,F=2,MF=0 =|5P1/2,F=2,MF=0 .
Dictating this choice was our desire for a particular relationship
between the scattering strengths for the different condensate
components, which control the processing. Here, the s-wave scattering
length for collisions between |2 .
Dictating this choice was our desire for a particular relationship
between the scattering strengths for the different condensate
components, which control the processing. Here, the s-wave scattering
length for collisions between |2 atoms is a22=5.36 nm, and the ratios between this quantity
and the scattering lengths for collisions between |1
atoms is a22=5.36 nm, and the ratios between this quantity
and the scattering lengths for collisions between |1 atoms and between |1
atoms and between |1 and |2
and |2 atoms are a11:a12:a22=0.95: 0.975:1.
There is no photon-induced recoil, and both condensate components
are trapped by the magnet.
atoms are a11:a12:a22=0.95: 0.975:1.
There is no photon-induced recoil, and both condensate components
are trapped by the magnet.
(c-d) Strong probe case. This
represents a different regime, where the probe and coupling laser
strengths are comparable. This leads to significant nonlinear
effects in the condensate dynamics, and associated nonlinear processing
of optical information is possible. When a probe light pulse is
input and stopped in the condensate (0 ms), a large fraction of
the atoms within the pulse region are transferred to |2 .
The corresponding depletion of the condensate of |1 .
The corresponding depletion of the condensate of |1 atoms is significant and influences the ensuing two-component
condensate dynamics, leading to the nonlinearities. In this case,
the two components phase-separate: the |1
atoms is significant and influences the ensuing two-component
condensate dynamics, leading to the nonlinearities. In this case,
the two components phase-separate: the |1 -condensate
component develops two dark solitons filled with state |2 -condensate
component develops two dark solitons filled with state |2 condensate atoms. The resulting density in the two components,
after 110 ms of evolution, is shown in (d), left panel. The coupling
laser is switched on at this time, and the revived probe pulse
is shown in the right panel (red curve). As is seen, the solitons
are written onto the probe light field. In this strong-probe case,
the coupling laser is significantly affected by the write process,
and it is really in the ratio of the two light field amplitudes
that the full result of the processing is contained. The solitons
correspond to large phase gradients in the condensate wavefunction,
and these phase gradients are also written onto the light fields
[15]. For these calculations, we used co-propagating probe and
coupling laser beams with opposite circular polarisations, but
now with frequencies of the laser fields tuned such that the states
of the L system are |1
condensate atoms. The resulting density in the two components,
after 110 ms of evolution, is shown in (d), left panel. The coupling
laser is switched on at this time, and the revived probe pulse
is shown in the right panel (red curve). As is seen, the solitons
are written onto the probe light field. In this strong-probe case,
the coupling laser is significantly affected by the write process,
and it is really in the ratio of the two light field amplitudes
that the full result of the processing is contained. The solitons
correspond to large phase gradients in the condensate wavefunction,
and these phase gradients are also written onto the light fields
[15]. For these calculations, we used co-propagating probe and
coupling laser beams with opposite circular polarisations, but
now with frequencies of the laser fields tuned such that the states
of the L system are |1 =|5S,F=1,MF=-1 =|5S,F=1,MF=-1 ,
|2 ,
|2 =|5S,F=1,MF=+1 =|5S,F=1,MF=+1 ,
and |3 ,
and |3 =|5P1/2,F=2,MF=0 =|5P1/2,F=2,MF=0 .
The scattering lengths are a11=a22=5.36
nm, and a12 =1.04 a11. The latter is larger
than the value for an isolated rubidium atom where a12
=1.005 a11. The larger value is chosen in order to
speed up the processing. Scattering lengths can be controlled
with external electric and magnetic fields. .
The scattering lengths are a11=a22=5.36
nm, and a12 =1.04 a11. The latter is larger
than the value for an isolated rubidium atom where a12
=1.005 a11. The larger value is chosen in order to
speed up the processing. Scattering lengths can be controlled
with external electric and magnetic fields.
|
There are then four long-lived vortices
remaining. The vortices first move towards the condensate edge, scatter,
and circle back towards the centre, which puts them on a collision course.
At 57 ms they collide and their paths make a sharp 90░ turn. The vortices
then circle back after colliding with the condensate boundaries, and
a second collision occurs after 122 ms, which gives rise to a sound
wave (the curved fronts at 123 ms) that is seen emanating from the centre.
We should be able to create a controlled many body
system of these 'vortex particles' as illustrated by the calculation
shown in Fig. 6b. Here, a light pulse, stopped at a light roadblock
in a pancake shaped BEC, causes a whole line of vortices to form on
both sides of the condensate. With the addition of a third dimension,
vortex rings and filaments replace these vortex point particles and
introduce a host of new and exciting dynamics as a result of the more
complicated topology.
Spatial modulation of the coupling laser [10] in
a slow light medium forms the basis for the proposed observation of
effects of general relativity in table-top, earth-based experiments
[27], and for recent photonic bandgap induced storage of light pulses
in atomic media [28].
Outlook
As described above, ultra-slow light allows for the ultimate control
of light: the manipulation, storage, and processing of optical information.
We imagine that ultra-slow light can be used as a basis for creating
dynamically controllable optical delay lines with large and variable
optical delays obtained in very small optical structures. The delays
and the bandwidth of such a system could be controlled simply through
control of the coupling laser intensity. It is important to note, that
temporal spreading, spatial distortion, and absorption are all minimised
for light-pulse propagation under ultra-slow light conditions because
of the linear variation of the refractive index with frequency around
its unity value at resonance.
The dramatic spatial pulse compression and coherent,
holographic imprinting of optical information in atomic media, associated
with ultra-slow light, led to the observation of stopped light. Using
this technique, we envision developing three-dimensional optical storage
devices with optical information stored in highly compressed form, and
the creation of optical shift registers controlled by the on/off switching
of a coupling laser with illumination in spatially selected regions.
Dynamical bandwidth control for transform limited pulse propagation
is possible, as is controlled coherent processing of optical information
through utilisation of the coherent dynamics of Bose-Einstein condensates.
Furthermore, ultra-slow-light-based output-coupling from condensates
of very localised coherent structures with controlled spatial shapes
and recoil momenta could be of great importance for atom-interferometry.
|
|
|
Fig 5 Light
Roadblock and Quantum Shock Waves in Bose-Einstein Condensates
(a)
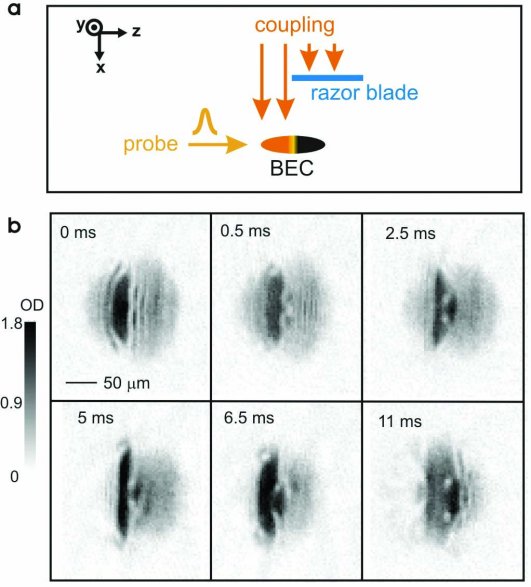
Light roadblock. A razor blade blocks the coupling beam from illuminating
the far (z>0) side of the condensate. When the slowed probe
light pulse reaches the roadblock (at z=0), where the coupling
intensity drops to zero, the light pulse is further slowed and
dramatically compressed to only a few microns, creating a narrow
imprint of |2 atoms in the condensate. This imprint is kicked out (as in Fig.
2) and leaves a condensate of state |1
atoms in the condensate. This imprint is kicked out (as in Fig.
2) and leaves a condensate of state |1 atoms trapped in the magnet, with a narrow density depletion in
the middle. The narrow defect results in the formation of two
density dips that propagate at the sound speed towards the condensate
boundaries. Due to the dramatic variation of atom density and
local sound speed across the structures, the back parts of the
dips will catch up to the central parts, and the back edges will
steepen. This process would in a normal fluid lead to shock wave
formation. Here, where we form the defects in a Bose-Einstein
condensate, we create the superfluid analogues of shock waves,
'quantum shock waves', in the form of topological defects (for
example, dark solitons).
atoms trapped in the magnet, with a narrow density depletion in
the middle. The narrow defect results in the formation of two
density dips that propagate at the sound speed towards the condensate
boundaries. Due to the dramatic variation of atom density and
local sound speed across the structures, the back parts of the
dips will catch up to the central parts, and the back edges will
steepen. This process would in a normal fluid lead to shock wave
formation. Here, where we form the defects in a Bose-Einstein
condensate, we create the superfluid analogues of shock waves,
'quantum shock waves', in the form of topological defects (for
example, dark solitons).
(b) Observation of quantum
shock waves at the light roadblock (from ref. 10). After the density
defect is formed at the light roadblock, we leave the condensate
of |1 atoms trapped in the magnet for a varying amount of time (as indicated
in the figures). We then abruptly turn the trap off and let the
cloud expand for 15 ms. We subsequently image the central slice
of the dropping condensate with the imaging beam (Fig. 1a) (the
vertical height (along y) of the slice is 30 Ám). We immediately
observe (at 0 ms) the appearance of a series of white stripes
(white means no condensate density), which indicate that dark
solitons have been formed. The solitons are unstable, and the
fronts are observed to curve after just 0.5 ms ('snake instability'
[31]). The points along the main front, with large curvature,
act as nucleation sites for quantized vortices, and at 2.5 ms
we observe that two vortices have formed (seen as white dots in
the figure). These two vortices are very stable, and they are
clearly seen at 11 ms, for example. In the process, the overall
shape of the condensate is also changing dramatically (indicating
the presence of a large collective excitation of the condensate).
At 5 ms the condensate is long, dense, and narrow. The condensate
subsequently relaxes into the extended shape seen at 11 ms.
atoms trapped in the magnet for a varying amount of time (as indicated
in the figures). We then abruptly turn the trap off and let the
cloud expand for 15 ms. We subsequently image the central slice
of the dropping condensate with the imaging beam (Fig. 1a) (the
vertical height (along y) of the slice is 30 Ám). We immediately
observe (at 0 ms) the appearance of a series of white stripes
(white means no condensate density), which indicate that dark
solitons have been formed. The solitons are unstable, and the
fronts are observed to curve after just 0.5 ms ('snake instability'
[31]). The points along the main front, with large curvature,
act as nucleation sites for quantized vortices, and at 2.5 ms
we observe that two vortices have formed (seen as white dots in
the figure). These two vortices are very stable, and they are
clearly seen at 11 ms, for example. In the process, the overall
shape of the condensate is also changing dramatically (indicating
the presence of a large collective excitation of the condensate).
At 5 ms the condensate is long, dense, and narrow. The condensate
subsequently relaxes into the extended shape seen at 11 ms.
|
Ultra-slow light also allows for extreme optics.
Nonlinear optical effects associated with slow light are so large [1,29]-due
to the steep refractive index profile-that nonlinear optics close to
the single photon level is possible with micron-sized structures. For
example, ultra-sensitive switches, with a switching energy corresponding
to just two photons (10-18 Joule), and frequency up-conversion at very
low power levels are possible.
|
|
|
Fig 6 Quantum
Shock Waves and Vortex Dynamics
(a)
Vortex dynamics. A numerical calculation of the dynamics for a
sodium condensate after a deep, narrow density defect has been
created at t=0 at a light roadblock. The dynamics are calculated
with the non-linear Gross-Pitaevskii equation [12], and the plots
show the density of the condensate at the times indicated. The
formation, dynamics, and interactions of the vortices formed by
the defect are discussed in the text. The size and amplitude of
the defect is controlled with the duration and intensity of the
probe pulse and in this case, a 100 % density defect, with a half-width
of 3 Ám, is imposed initially, and this leads to formation of
4 long-lived vortices that first collide like billiard balls (at
57 ms) and then scatter off the condensate boundaries. A second
collision (at 122 ms) results in the creation of a large spherically
outgoing sound wave (123 ms).
(b) Many-body system of vortices.
Numerical calculation of the dynamics for a condensate, trapped
in a spherically symmetric magnetic field, after a defect with
half-width 2.3 Ám is imposed. We see that the deepest solitons
break up into ten vortices each. The number of vortices formed
is determined by the intensity and duration of the probe pulse,
and the light roadblock is therefore ideal for controlled studies
of many-body systems of vortices.
|
With use of the light roadblock, light
pulses have been compressed to sizes comparable to the wavelength of
light, a very interesting regime for further studies. Furthermore, creation
of vortices at the light roadblock makes possible unprecedented and
direct studies of vortex collision dynamics in superfluids. Superfluidity
is a property which allows BECs to flow without dissipation, and equivalently,
superconductors to conduct currents with no resistance. Vortex collisions
are expected to form the main mechanism by which dissipation is introduced
into superfluid systems and are therefore of fundamental importance
for understanding the breakdown of superfluidity and superconductivity.
Acknowledgement
The research was supported by the U.S. Airforce Office of Scientific
Research, the U.S. Army Research Office OSD Multidisciplinary University
Research Initiative Program, The National Science Foundation, and the
National Aeronautics and Space Administration. CS was supported by a
National Defense Science and Engineering Fellowship sponsored by the
U.S. Department of Defense.
About the author
Lene Vestergaard Hau is Gordon McKay Professor of Applied Physics and
Professor of Physics at Harvard University. She received her Ph.D. from
the University of Aarhus, Denmark. She was named MacArthur Fellow in
2001 and just received the 2004 Richtmyer Memorial Lecture Award.
References
[1] Hau, L.V., Harris, S.E., Dutton, Z., and Behroozi, C.H., Light
speed reduction to 17 metres per second in an ultracold atomic gas.
Nature 397, 594-598 (1999).
[2] Inguscio, M., Stringary, S., and Wieman, C., eds., Bose-Einstein
Condensation in Aomtic Gases, Proceedings of the International School
of Physics Enrico Fermi, Course CXL, (International Organisations
Services, Amsterdam, 1999).
[3] Hau, L.V. Bose-Einstein condensation and light speeds of 38 miles/hour,
in proceedings from the Workshop on Bose-Einstein Condensation and Degenerate
Fermi Gases, Feb. 10-12, 1999 (Centre for Theoretical Atomic, Molecular,
and Optical Physics, Boulder, CO) http://fermion.colorado.edu/~chg/Talks/Hau
[4] Liu, C., Dutton, Z., Behroozi, C.H., and Hau, L.V., Observation
of coherent optical information storage in an atomic medium using halted
light pulses. Nature 409, 490-493 (2001).
[5] Kash, M.M., et al., Ultraslow group velocity and enhanced
nonlinear optical effects in a coherently driven hot atomic gas. Phys.
Rev. Lett. 82, 5229-5232 (1999).
[6] Budker, D., Kimball, D.F., Rochester, S.M., Yashchuk, V.V., Nonlinear
magneto-optics and reduced group velocity of light in atomic vapour
with slow ground state relaxation. Phys. Rev. Lett. 83,
1767-1770 (1999).
[7] Phillips D.F., Fleischhauer, A., Mair, A., Walsworth, R.L., and
Lukin, M.D., Storage of light in atomic vapour. Phys. Rev. Lett.
86, 783-786 (2001).
[8] Turukhin, A.V., et al., Observation of ultraslow and stored light
pulses in a solid. Phys. Rev. Lett. 88, 023602 (2002).
[9] Bigelow, M.S., Lepeshkin, N.N., and Boyd, R.W., Observation of
Ultraslow Light Propagation in a Ruby Crystal at Room Temperature. Phys.
Rev. Lett. 90, 113903-1 (2003).
[10] Dutton, Z., Budde, M., Slowe, C., and Hau, L.V., Observation of
quantum shock waves created with ultra-compressed slow light pulses
in a Bose-Einstein Condensate. Science 293, 663-668 (2001).
[11] Harris, S.E., Electromagnetically induced transparency. Physics
Today 50, 36-42 (1997).
[12] Dalfovo , F., Giorgini, G., Pitaevskii , L.P., and Stringari ,
S., Theory of Bose-Einstein condensation in trapped gases. Rev. Mod.
Phys. 71, 463-512 (1999).
[13] Gustavson, T. L., Landragin, A., Kasevich, M. A., Rotation sensing
with a dual atom-interferometer Sagnac gyroscope. Classical Quant.
Grav. 17, 2385-2398 (2000).
[14] Snadden, M. J., McGuirk, J. M., Bouyer, P., Haritos, K. G., Kasevich,
M. A., Measurement of the earth's gravity gradient with an atom interferometer-based
gravity gradiometer. Phys. Rev. Lett. 81, 971-974 (1998); Peters,
A., Chung, K. Y., Chu, S., Measurement of gravitational acceleration
by dropping atoms. Nature 400, 849-852 (1999).
[15] Dutton, Z. and Hau, L.V., in preparation.
[16] Dutton, Z., Ph.D. Thesis, (Harvard University, 2002).
[17] Burger, S., Bongs, K., Dettmer, S., Ertmer, W., and Sengstock,
K., Dark Solitons in Bose-Einstein Condensates. Phys. Rev. Lett.
83, 5198-5201 (1999).
[18] Manakov, S.V., On the theory of two-dimensional stationary self-focusing
of electromagnetic waves. Soviet Phys. JETP 38, 248-253
(1974).
[19] Busch, T., Anglin, J.R., Dark-bright solitons in inhomogeneous
Bose-Einstein condensates. Phys Rev. Lett. 87, 010401
(2001).
[20] Inouye, S., et al., Observation of Feshbach resonances in a Bose-Einstein
condensate. Nature 392,151-154 (1998).
[21] Cornish, S.L., Claussen, N.R., Roberts, J.L., Cornell, E.A., and
Wieman, C.E., Stable Rb-85 Bose-Einstein condensates with widely tunable
interactions. Phys. Rev. Lett. 85, 1795-1798 (2000).
[22] M. Kitagawa and M. Ueda, Squeezed spin states. Phys. Rev. A
47, 5138-5143 (1993).
[23] Sorensen, A., Duan, L.-M., Cirac, J.I., and Zoller, P., Many-particle
entanglement with Bose-Einstein condensates. Nature 409,
63-66 (2001).
[24] Lukin, M.D., Yelin, S.F., and Fleischhauer, M., Entanglement of
atomic ensembles by trapping correlated photon states. Phys. Rev.
Lett. 84, 4232-3235 (2000).
[25] DiVincenzo, D.P., The physical implementation of quantum computation,
Fortsch. Phys. 48, 771-783 (2000).
[26] Donnelly, R.J., Quantized vortices in Helium II, (Cambridge
Univ. Press, Cambridge, 1991).
[27] Leonhardt, U., A laboratory analogue of the event horizon using
slow light in an atomic medium, Nature 415, 406 (2002).
[28] Bajcsy, M., Zibrov, A. S., Lukin, M. D., Stationary pulses of
light in an atomic medium, Nature 426, 638 (2003).
[29] Harris, S.E. and Hau, L.V., Nonlinear optics at low light levels,
Phys. Rev. Lett., 82, 4611 (1999).
[30] Myatt, C.J., Burt, E.A., Ghrist, R.W., Cornell, E.A., and Wieman,
C.E., Production of Two Overlapping Bose-Einstein Condensates by Sympathetic
Cooling. Phys. Rev. Lett. 78, 586-589 (1997).
[31] Anderson, B.P., et al., Watching dark solitons decay into vortex
rings in a Bose-Einstein condensate. Phys. Rev. Lett. 86,
2926-2929 (2001).
Copyright EPS
and EDP Sciences,
2004
|